The Course

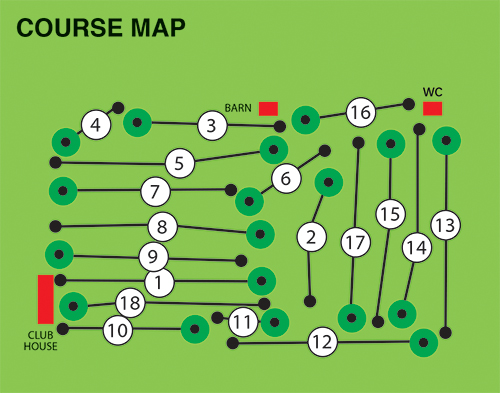
Hole five, nicknamed redoubted is a par 5 that is four hundred and fifty-five meters from the blue tee and three hundred and seventy-five meters from the women’s tee to the center of the green. This is stroke three for men, and stroke five, for women. A good tee shot down the right-hand side of the fairway gives up a chance of hitting the green in two. If laying up, it is recommended to give yourself a full shot in to avoid getting caught up in the humps short.  The green slopes severely from back to front leaving an ultra-fast chip or putt if long.